import numpy as np
import numba as nb
import matplotlib.pyplot as plt
import mpmath as mp
# naive implementation
def msq1(px1, py1, pz1, px2, py2, pz2, m1, m2):
p1_sq = px1 ** 2 + py1 ** 2 + pz1 ** 2
p2_sq = px2 ** 2 + py2 ** 2 + pz2 ** 2
m1_sq = m1 ** 2
m2_sq = m2 ** 2
# energies of particles 1 and 2
e1 = np.sqrt(p1_sq + m1_sq)
e2 = np.sqrt(p2_sq + m2_sq)
# dangerous cancelation in third term
return m1_sq + m2_sq + 2 * (e1 * e2 - (px1 * px2 + py1 * py2 + pz1 * pz2))
# numerically stable implementation
@nb.vectorize
def msq2(px1, py1, pz1, px2, py2, pz2, m1, m2):
p1_sq = px1 ** 2 + py1 ** 2 + pz1 ** 2
p2_sq = px2 ** 2 + py2 ** 2 + pz2 ** 2
m1_sq = m1 ** 2
m2_sq = m2 ** 2
x1 = m1_sq / p1_sq
x2 = m2_sq / p2_sq
x = x1 + x2 + x1 * x2
a = angle(px1, py1, pz1, px2, py2, pz2)
cos_a = np.cos(a)
if cos_a >= 0:
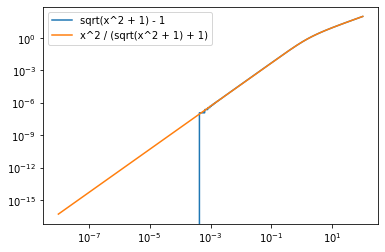
y1 = (x + np.sin(a) ** 2) / (np.sqrt(x + 1) + cos_a)
else:
y1 = -cos_a + np.sqrt(x + 1)
y2 = 2 * np.sqrt(p1_sq * p2_sq)
return m1_sq + m2_sq + y1 * y2
# numerically stable calculation of angle
@nb.njit
def angle(x1, y1, z1, x2, y2, z2):
# cross product
cx = y1 * z2 - y2 * z1
cy = x1 * z2 - x2 * z1
cz = x1 * y2 - x2 * y1
# norm of cross product
c = np.sqrt(cx * cx + cy * cy + cz * cz)
# dot product
d = x1 * x2 + y1 * y2 + z1 * z2
return np.arctan2(c, d)
rng = np.random.default_rng(1)
dtype = np.float32
size = 10000
px1 = (10 ** rng.uniform(0, 5, size=size) * rng.choice([-1, 1], size=size)).astype(dtype)
py1 = (10 ** rng.uniform(0, 5, size=size) * rng.choice([-1, 1], size=size)).astype(dtype)
pz1 = (10 ** rng.uniform(0, 5, size=size) * rng.choice([-1, 1], size=size)).astype(dtype)
px2 = (10 ** rng.uniform(0, 5, size=size) * rng.choice([-1, 1], size=size)).astype(dtype)
py2 = (10 ** rng.uniform(0, 5, size=size) * rng.choice([-1, 1], size=size)).astype(dtype)
pz2 = (10 ** rng.uniform(0, 5, size=size) * rng.choice([-1, 1], size=size)).astype(dtype)
m1 = 10 ** rng.uniform(-5, 5, size=size).astype(dtype)
m2 = 10 ** rng.uniform(-5, 5, size=size).astype(dtype)
# as reference we use naive formula computed with mpmath
M0 = []
with mp.workdps(100):
for px1i, py1i, pz1i, px2i, py2i, pz2i, m1i, m2i in zip(px1, py1, pz1, px2, py2, pz2, m1, m2):
px1i = mp.mpf(float(px1i))
py1i = mp.mpf(float(py1i))
pz1i = mp.mpf(float(pz1i))
px2i = mp.mpf(float(px2i))
py2i = mp.mpf(float(py2i))
pz2i = mp.mpf(float(pz2i))
m1_sq = mp.mpf(float(m1i)) ** 2
m2_sq = mp.mpf(float(m2i)) ** 2
e1 = mp.sqrt(px1i ** 2 + py1i ** 2 + pz1i ** 2 + m1_sq)
e2 = mp.sqrt(px2i ** 2 + py2i ** 2 + pz2i ** 2 + m2_sq)
M0.append(float(m1_sq + m2_sq + 2 * (e1 * e2 - (px1i * px2i + py1i * py2i + pz1i * pz2i))))
M0 = np.array(M0)
M = {f.__name__: f(px1, py1, pz1, px2, py2, pz2, m1, m2) for f in (msq1, msq2)}
fig, ax = plt.subplots(1, len(M), figsize=(len(M) * 4.5, 4), sharey=True)
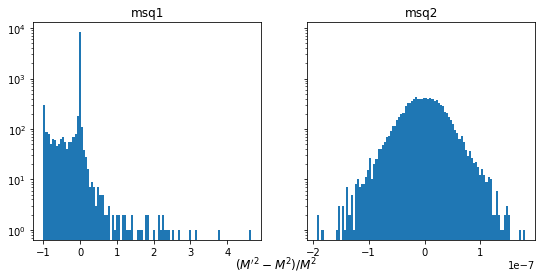
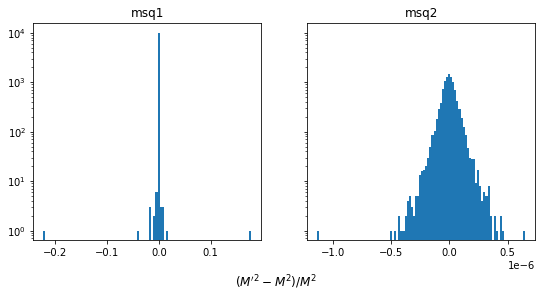
for (fname, Mi), axi in zip(M.items(), ax):
d = (Mi - M0) / M0
axi.hist(d, bins=100)
axi.set_yscale("log")
axi.set_title(f"{fname}")
fig.supxlabel(r"$(M'^2 - M^2) / M^2$", y=-0.05);